KOMENTÁRE K RIEŠENIAM 3. SÉRIE ÚLOH KOMINÁRA 2001/2002

Posledné kolo seminára prinieslo ohromný boj o prvých 5 miest výsledkovej listiny. Nakoniec v tomto boji zaslúžene zvíťazil Vlado Boža, ale naše uznanie si zaslúžite všetci, ktorí ste sa úspešne či neúspešne ale v duchu pravidiel popasovali s 15 úlohami, čo sme vám pre tento ročník pripravili. Vaše anketové názory potvrdili, že v 3. sérii úloh boli tri ľahšie príklady (1,3,5) a dva ťažšie (2,4). Kým úloha č.1 sa vám zväčša javila ako ľahká a zároveň pekná,  tak úloha č.2 práve naopak škaredá a ťažká. Zvýšenú pozornosť zaznamenala aj úloha č.4, ktorá napriek tomu, že bola ťažká sa vám mnohým aj páčila. Výsledky ankety :

1. Úlohu o Bitangovi, Podfukovi a Švindľovi ste riešili buď sústavou rovníc alebo ste problém rozobrali od konca. Na konci mali totiž všetci traja Bitkovia rovnaký počet lístkov. Ak ich spolu bolo 96, tak každý z nich musel mať 32 lístkov. Pri poslednom prerozdelení dostal Podfuk od Bitanga toľko lístkov, koľko práve mal. Jeho počet sa teda zdvojnásobil. Ak dvojnásobok je 32, tak pred posledným prihadzovaním mal Podfuk 32:2=16 lístkov a Bitang 32+16=48 lístkov. Tento počet však Bitang dosiahol pri druhom prerozdelení, keď dostal od Švindľa toľko lístkov, koľko dovtedy mal. Takže pred druhým prihadzovaním mal Bitang  48:2=24 lístkov a Švindeľ 32+24=56 lístkov. Švindeľ však na začiatku dostal od Podfuka toľko lístkov, koľko dovtedy mal, a to je tentokrát polovica z 56, čiže 28 lístkov. Podfuk preto musel mať na začiatku 16+28=44 lístkov, Švindeľ 28 lístkov a Bitang 24 lístkov. Pre kontrolu 44+28+24=96.

2. Kominársky škriatok sa nám tentokrát vlúpal do druhej úlohy. Vďaka nemu a MS Wordu – počítačovému programu, v ktorom zadania úloh tvoríme sa nám podarilo umiestniť gule do špeciálnej polohy. Nájdenie riešenia pre daný obrázok to silne uľahčilo, avšak mnohých z vás to odviedlo od hľadania riešenia pre akékoľvek počiatočné postavenie gúľ. Napríklad takéto.

Vlado Boža, Majka Jirásková, Jakub Blaško a Lucia Fedorová sa však nenechali popliesť a poslali nám riešenie vhodné pre všetky prípustné počiatočné postavenia gúľ. Riešenie využíva vlastnosti osovej súmernosti. Označme body, kde sa guľa odrazí od ľavého, horného, pravého a dolného okraja stola postupne L,H,P,D. Označme 1´ bod súmerne združený s guľou 1 podľa ľavého okraja stola a symbolom 1´´ bod súmerne združený s bodom 1´ podľa osi prechádzajúcej horným okrajom stola. Podobne označme 2´ bod súmerne združený s guľou 2 podľa spodného okraja stola a symbolom 2´´ bod súmerne združený s bodom 2´ podľa osi prechádzajúcej pravým okrajom stola. 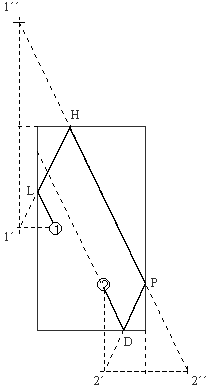Situáciu znázorňuje ďalší obrázok. V obrázku je znázornená konštrukcia lomenej čiary 1-L-H-P-D-2. Najprv spojíme body 1´´ a 2´´. Priesečníky s okrajmi stola sú body H a P. Priesečník spojnice P a 2´ je bod D, priesečník spojnice H a 1´ je bod L. Táto konštrukcia zaručuje zhodnosť uhlov dopadu a odrazu, pričom výsledná lomená spája body 1 a 2. Všimnite si, že v tomto prípade počiatočného rozmiestnenia gúľ predĺženie spojnice bodov 2 a D neprechádza bodom 1.

 3. V úlohe o zápalkovej hre Bitpolka, ktorej riešenie sa v ankete nikomu nezdalo ťažké, ste zistili, že existujú prehrávajúce pozície 2, 5, 11, 23, 47, ... zápaliek, kde každý ďalší nevýhodný počet zápaliek na kope zapíšeme pomocou predchádzajúceho takto X₁=2, X_n = 2 . X_n-1 + 1. Janko Geroč dokonca objavil vzorec X_n = 2ⁿ + 2^n-1 - 1, v ktorom nemusím poznať predchádzajúce nevýhodné číslo. Hráči sa snažia odobrať taký počet zápaliek, aby súperovi ostal na kope nevýhodný počet zápaliek a nech robí čo robí, ďalším ťahom ho vieme dostať do nasledujúcej nevýhodnej pozície. Ak zoberieme do úvahy pripomienku Martina Bachratého, že posledná zápalka sa nedá podľa pravidiel zobrať, potom posledná zápalka, ktorú z kopy v rámci hry zoberieme je zápalka z dvojzápalkovej kopy. Potom sa nevýhodné pozície posunú na 3, 7, 15, 31, ... takže pre ne platí vzorec X₁=3, X_n = 2 . X_n-1 + 1 alebo X _n = 2ⁿ  - 1 pre n>1.

4. Skláňame sa nielen pred majstrovstvom slovenských hokejistov ale tentokrát hlavne pred riešiteľmi Kominára, najmä tými nehokejovými, ktorí sa nevzdali pred ťažkosťami tejto úlohy. V prvom rade ste zvyčajne určili, že družstvo Juhu dostalo v turnaji 4 góly. Počet gólov, ktoré na turnaji všetky tímy spolu dali musí byť rovnaký ako počet všetkých gólov, ktoré mužstvá od súperov dostali, teda 6+2+3+1=1+4+3+X  => X=4. Ak Južania hrali 3 zápasy, dvakrát remizovali a majú nepriaznivé skóre 1:4, potom je jasné, že tretí zápas museli prehrať. Spodný riadok tabuľky teda vyzerá takto :

Ďalej vieme, že na turnaji, kde hral každý s každým sa odohralo 6 zápasov a v nich sa rozdalo 12 bodov. Vieme tiež, že Západ na treťom mieste musí mať najmenej 2 body a Východ  kvôli horšiemu skóre vždy aspoň o bod viac. Ak by mal Západ 3 body, Východ so Severom by museli mať aspoň 4 body a celkový súčet bodov 2+3+4+4 by prekročil 12. Z toho vyplýva, že Západ musí mať tiež dva body a nemôžu to byť body za dve remízy, pretože tretí zápas by Západ musel prehrať a nemohol by mať celkovo vyrovnané skóre. Západ teda raz vyhral a dvakrát prehral a tretí riadok tabuľky vyzerá takto :

Vieme už aj určiť výsledok zápasu Západ-Juh. Keďže Západ nemá žiadnu remízu, musel nad Juhom zvíťaziť. Juh má podľa skóre na konte prehru o 3 góly a prehrať so Západom o 3 góly mohol jediným spôsobom Západ – Juh 3:0. Vieme už tiež, že Juh remizoval so Severom aj s Východom a Západ s oboma týmito družstvami prehral. Keďže vieme o jednom víťazstve a jednej remíze mužstva Východu, jeho nepriaznivé celkové skóre prezrádza, že Východ musel aj prehrať a to s tímom Severu. Tým sa nám vyjasnila celá tabuľka.

Ostáva ešte určiť výsledky piatich stretnutí. Východ nad Západom zvíťazil a teda určite mu strelil aspoň jeden gól. Ten druhý nemohol streliť Severu, pretože Sever dostal len jediný gól a preto by Sever musel s Juhom remizovať 0:0 a Východ s Juhom 1:1. Lenže to by už bol tretí strelený gól Východu a vieme, že Východ ich v turnaji strelil len dva. Ten druhý nemohol streliť ani Juhu, pretože potom by Juh musel remizovať so Severom 0:0, o Západe vieme, že svoje 3 góly dal Juhu a Severu by už nemal kto dať ten jediný gól. Z toho všetkého vychádza že aj druhý gól vsietil Východ do bránky Západu, takže Východ – Západ 2:0 a hneď je už jasný aj posledný výsledok Západu Sever – Západ 1:0. Pretože Východ dal oba svoje góly Západu, s Juhom musel remizovať bez gólov, teda Východ – Juh 0:0, odtiaľ hneď dostávame posledný výsledok Južanov Sever – Juh 1:1 a teraz už aj posledný dá sa povedať finálový výsledok celého turnaja Sever – Východ 4:0.

5.  Honba za pokladom Jeana de Mijóna dopadla úspešne. Prevažne hravo ste rozlúskli, že cestou za pokladom musíte prejsť :

100 krokov rovno

otočiť sa vľavo bok

znova 100 krokov rovno

otočiť sa vľavo bok

ešte raz 100 krokov rovno

otočiť sa vľavo bok

kopať až kým nevykopeme poklad

              (alebo nevypadneme dierou  na druhej strane zemegule)

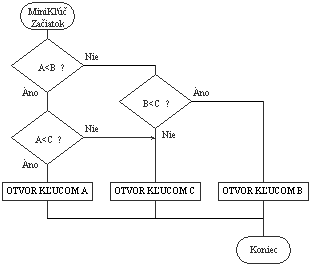
Vývojový diagram pre šamana Johana mohol vyzerať rôzne, pretože neboli jasne zadefinované príkazy, zväčša ste urobili to, čo sme od vás očakávali a to svedčí o tom, že ste šikovní vývojári. Ako príklad uvedieme najčastejšie riešenie.

KOMENTÁRE K RIEŠENIAM 1. SÉRIE ÚLOH KOMINÁRA 2001/2002

Podľa dosiahnutých výsledkov aj vašej ankety bola ťažšia len úloha č.3. S ostatnými ste sa zväčša vysporiadali viacmenej bez problémov. Tešíme sa všetkým novým riešiteľom a vítame ich v našom Bitlandskom svete. Tým, ktorí si už na nás nenašli čas odkazujeme, že nikdy nie je neskoro zapojiť sa. Každý riešiteľ bude pozvaný na letnú výpravu na Bitland. Tento rok je predpokladaný termín tábora 18.-27.8. a cena pobytu nepresiahne 1500,- Sk. Pozvánky a presnejšie informácie dostanete s výsledkami druhej série úloh.

Výsledky ankety :

Miss krásy  získala úloha č.1 (8 hlasov).

Zato v súťaži o najškaredšiu úlohu „zvíťazila“ jednoznačne úloha č. 3 (7 hlasov).

Najľahšia bola úloha č.1 (7 hlasov).

A najťažšia bola opäť úloha č.3 (6 hlasov).

Najextrémnejšia bola, čiže najviac hlasov zo všetkých Naj mala úloha č.1 (spolu 17 hlasov).

1. V úlohe o bitlandských veštkyniach ste ukázali, že vás nikto len tak ľahko neoklame. Správne ste identifikovali, že pohraničiarky sedeli v poradí zľava Roxana, Saxana a Doloréz. Možných postupov pátrania bolo niekoľko. Asi ten najjednoduchší a bezchybný sme si na ukážku požičali od Janka Geroča: „Ľavá povedala, že uprostred sedí Doloréz. Prostredná však povedala, že je Roxana. A pretože Doloréz vraví vždy pravdu, určite nesedela Doloréz vľavo ani uprostred. Doloréz sedela teda vpravo. Keby sedela inde, tak by klamala. Pravá, teda Doloréz, povedala, že vedľa nej sedí Saxana. Keďže vraví pravdu, tak Saxana sedela uprostred. Posledná ostáva Roxana, ktorej ostáva už len miesto vľavo. V dialógu s Ferom (Fredym) klamali ľavá aj prostredná, pravdu vravela iba pravá, čiže Doloréz.“ Mnohí ste zabudli napísať toto overenie. V prípade, že by sa ukázalo, že Saxana vravela pravdu, úloha by nemala riešenie.

2. V geometrickej úlohe o satelitných transportéroch ste zväčša správne pochopili, že jedna nádoba so špeciálnou tekutinou zaplní priestor transportéra štvorcového prierezu so stranou dĺžky jednej tyče. Ak transportér musí mať vždy 12 tyčí,  to v prípade pravouhlého uzavretého obrazca je vždy útvar vyplniteľný piatimi nádobami. Úlohou je, ako zmenšiť obsah obrazca z 5 na 4 resp. 3 pri nezmenenom obvode 12 tyčí. Najčastejšie ste použili náhradu úsečky o dĺžke jednej tyče lomenou čiarou so 60° uhlami, ale našli sa aj iné nápady. Tu je niekoľko vašich riešení.

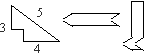Transportéry s obsahom 4 nádob

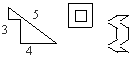Transportéry s obsahom 3 nádob

3. Tretia úloha vám zobrala asi najviac času a námahy. Preto hoci to bola celkom zaujímavá hra zvíťazila v ankete v kategóriách Miss Fúj a Miss Slon. Vaše riešenia boli veľmi rôznorodé – od 3 slov až po 35 strán. Veľkolepý rozpis všetkých možností Vlada Božu sa stal veľmi žiadaným aj na bitlandskom kráľovskom dvore. Či sa dostane do vzácnej zbierky Bitlandu, uvidíme v lete. Pri skúmaní riešení však stačilo, ak pre hráča, o ktorom tvrdíme, že vyhrá, nájdeme aspoň jeden ťah, na ktorý súper nech robí čo robí nenájde účinnú protizbraň.

Vyhrávajúce pozície druhého hráča :

Vyhrávajúce pozície prvého hráča :

Druhý hráč má výhodu, pretože má vyhrávajúcu stratégiu, ak na začiatku padne č. 1, 2, 5 alebo 6, kým prvý len ak na začiatku padne č.3 alebo 4.

 4. V úlohe o magických chvíľach bolo potrebné zistiť niekoľko dôležitých poznatkov :

                1, Magické chvíle môžu nastať len v symetrických rokoch a to sú v skúmanom

    intervale roky

            1001, 1111, 1221, 1331, 1441, 1551, 1661, 1771, 1881, 1991, 2002

                2, Mesiace musia byť symetrické s hodinami. Keďže mesiace majú čísla od 01 do 12

                  a hodiny od 00 do 23, vyhovujú takéto dvojice

                           01 – 10, 02 – 20, 10 – 01, 11 – 11, 12 – 21

3, Dni musia byť symetrické s minútami. Pretože minúty sú čísla od 00 do 59, dni

    s nimi symetrické môžu mať na konci najviac číslicu 5. Dní je najviac 31, takže

    prípustné dvojice sú

                            01 – 10, 02 – 20, 03 – 30, 04 – 40, 05 – 50,

                            10 – 01, 11 – 11, 12 – 21, 13 – 31, 14 – 41, 15 – 51,

                            20 – 02, 21 – 12, 22 – 22, 23 – 32, 24 – 42, 25 – 52,

                            30 – 03, 31 – 13

Pri  zisťovaní všetkých prípustných kombinácií dní, mesiacov, rokov, hodín a minút vynecháme zatiaľ rok 2002, ktorý nemôžeme zahrnúť celý a dni 30 a 31, ktoré nie sú v každom mesiaci. Takže bez obmedzenia môžeme skombinovať 17 dní a minút s 5 mesiacmi a hodinami a s 10 rokmi. To je spolu

                                               17 . 5 . 10 = 850

Spomedzi piatich mesiacov, v ktorých mohla nastať magická chvíľa, majú štyri 30. deň a tri aj 31.deň

                                               1 . (4+3) . 10 = 70

Za rok 2002 do 25.3. pribudnú ešte magické chvíle z mesiaca január (19) a mesiaca február (17).

Od 1.1.1000 do 25.3..2002 bolo spolu 850+70+19+17=956 magických chvíľ.

5. Posledná – programátorská úloha patrila k tým ľahším. Prevažne správne ste určili, že program 6 krát prebehne cyklus, v ktorom šuflík  N zmení postupne svoju hodnotu zo 7 na 6, 5, 4, 3, 2, 1 a v šuflíku Výsledok sa na začiatku vložená hodnota 1 postupne nahradí číslami 7, 42, 210, 840, 2520, 5040. Po skončení programu obsahuje šuflík Výsledok hodnotu 5040.