- V mnohých kráľovstvách je najcennejšie
zlato. V jednom kráľovstve prišli na to, že cennejšia je soľ. V kráľovstve
Bitland je však najcennešia informácia. Všetky informácie majú zapísané v knihách
a knihy starostlivo uložené vo všelijakých knižniciach. Kráľ Pentijak
I. sa bez knihy ani nepohne, neznáša však knihy s neočíslovanými stránkami
(môže z nich dostať aj infarkt).
Raz požiadal lorda Worda, aby mu očísloval jeho obľúbenú knihu "Ako chutí
moc". Lord Word vyfasoval v kráľovskom sklade 10 pečiatok s číslicami
0, 1, 2, 3, ... 9 a začal rýchlo číslovať. Keďže v tomto kráľovstve
všetci radi počítajú, napočítal, že musel
buchnúť razítkom spolu 345 krát. Kráľ sa mu bohato odmenil. Za každú očíslovanú
stranu dostal lord Word 1 bilár a navyše špeciálny príplatok 1 bilár
za každý úder pečiatkou "1", ktorú myši tak obhrýzli, že si pri jej razení
musel pomáhať kladivom. Koľko bilárov si zarobil lord
Word ?

- Lord Word si posledným úderom kladivom
po pečiatke s číslicou "1" tak nešťastne udrel po palci, že takmer polovicu
zárobku minul na liečenie v kráľovskej nemocnici. Preto sa rozhodol skoncovať
s myšami a do kráľovského skladu nasadil mačku Micu. Pretože sám
sa myší veľmi bál a navyše bol pohodlný, vymyslel pre Micu špeciálny
labyrint na kŕmenie. Kráľovský sklad sa nachádza v pivnici hradu hneď
vedľa hladomorne a je prepojený s komnatami
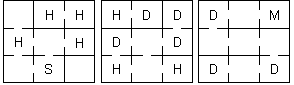
na prízemí a 1.poschodí niekoľkými rebríkmi. Rebríky sú v priloženom
plániku označené písmenami H (rebrík hore) a D (rebrík dole), sklad je
označený písmenom S a miska písmenom M. Zistite, aký najmenší počet
komnát musí Mica prejsť na ceste zo skladu k miske.
|
<<< D <<<<<<<<<<<
D <<<
|
|
Pivnica >>> H > Prízemie >>>
H >> 1.posch.
|

- Mačka Mica veru porobila s myšami
poriadky a dostala aj kráľovské vyznamenanie, ktoré kráľ Pentijak I.
odobral hradnej stráži. Predsa stráži nesmie do hradu prekĺznuť ani myš. Aby
zabezpečil dokonalú stráž svojho paláca požiadal kráľ svojho dvorného špecialistu
na počítače Bitka Kompíka, aby zostrojil robota strážcu. A veru
o pár týždňov bol na svete novučičký robot KAROL. Bitko Kompík dlho premýšľal,
ako ho naučiť vykonávať úlohu strážcu. Nakoniec ho naučil, aby rozumel niekoľkým
príkazom. Keď mu pošepol do plechového ucha "KROK", Karol urobil krok a Kompík
sa veľmi potešil.
Svoj povel zopakoval a Karol urobil druhý krok. Roboti totiž počúvajú
na 1.slovo. Ďalší príkaz, ktorý mu dal poriadne zabrať bol príkaz "VĽAVO VBOK".
Ale podarilo sa a Karol začal robiť obraty vľavo jedna radosť. Tu si
Kompík uvedomil, že nebude Karlovi
pripájať ďalšie zložité elektronické moduly, aby ho naučil robiť obraty
"Čelom vzad" a "Vpravo vbok". Tieto príkazy ho naučil robiť zloženým povelom.
Napr. zložený povel "Čelom vzad" vyzerá takto :
|
ČELOM VZAD
=
|
VĽAVO VBOK
|
|
|
VĽAVO VBOK
|
|
Koniec ČELOM
VZAD
|
|
Vašou prvou úlohou v tomto príklade je napísať, ako
Kompík naučil Karla vykonávať povel "Vpravo vbok".
Dôležité je, že všetky naučené zložené povely si už KAROL
navždy zapamätá.
Potom sa Kompík rozhodol
poslať Karla na prvú prechádzku. Aby však prechádzka nebola príliš krátka,
alebo zložený povel príliš dlhý, naučil ho ešte jeden príkaz, a to príkaz
"OPAKUJ POVEL N-KRÁT", kde N znamená počet opakovaní zadaného príkazu. Ak
chceme, aby Karol opakoval povel až do úplného vybitia svojich batérií,
počet opakovaní vynecháme. Zložený
povel "Prechádzka" na 20 krokov potom vyzeral takto :
|
PRECHÁDZKA =
|
OPAKUJ KROK 20 KRÁT
|
|
|
|
ČELOM VZAD
|
|
|
OPAKUJ KROK 20 KRÁT
|
|
Koniec PRECHÁDZKA
|
|
|
A Karol
sa veru naozaj prešiel 20 krokov tam a 20 krokov späť. Vašou druhou
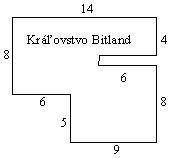
úlohou je vymyslieť zložený povel "OBCHÔDZKA", pomocou ktorého bude
Karol až do vybitia batérií obchádzať okolo hradieb kráľovstva podľa
plániku na obrázku. Čísla uvedené v plániku znamenajú
počet krokov potrebných na prejdenie okolo príslušnej steny.
|

- Ako každá krajina, aj Bitland má svoj
kráľovský trezor a v ňom ukrytý poklad nesmiernej ceny. Zámok trezoru
je však kódovaný špeciálnym kódovacím algoritmom. Otrhaný ale prefíkaný Bitko
Sisko trpí neskonalou túžbou odkódovať zámok a stať sa najbohatším obyvateľom
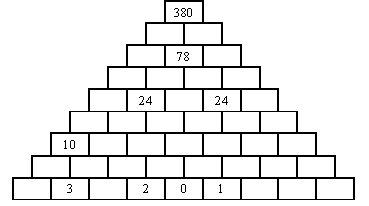
Bitlandu. Zatiaľ sa mu podarilo zistiť, že kódovací systém v tvare pyramídy
má na niektorých políčkach tzv. pevné kódy a pre celú
pyramídu platí kódovací predpis
![]()
![]()
![]()